Scientists develop method to help epidemiologists map spread of COVID-19

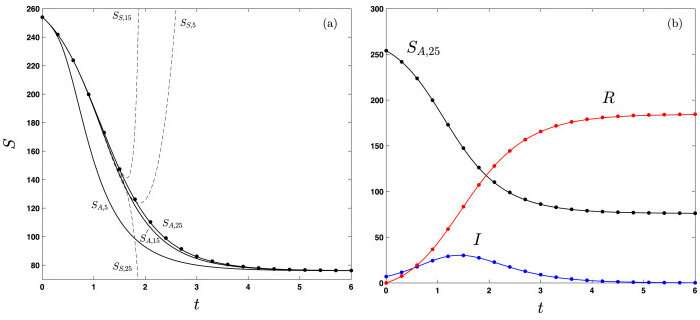
Rochester Institute of Technology scientists have developed a method they believe will help epidemiologists more efficiently predict the spread of the COVID-19 pandemic. Their new study, published in Physica D: Nonlinear Phenomena, outlines a solution to the SIR epidemic model, which is commonly used to predict how many people are susceptible to, infected by, and recovered from viral epidemics.

The method was created by Nathaniel Barlow, associate professor in RIT's School of Mathematical Sciences, and Steven Weinstein, head of RIT's Department of Chemical Engineering. They say that by using this solution to the model, epidemiologists can quickly forecast many different scenarios of how COVID-19 could spread based on a variety of variables. Projections produced by mathematical models help public officials make policy decisions about when to impose and lift restrictions aimed at flattening the curve of infection rates.

The applied mathematicians who developed the method said they were excited to find a way to apply their skills to help combat the pandemic.

"I was at home thinking that I would like to somehow help with everything going on," said Barlow. "We saw a popular article out there about the SIR model, saw that our method could speed the process up and we quickly wrote the paper. Our goal was to get better tools to the experts who are fighting this disease."

The method was based on solutions they previously developed to very different problems in thermodynamics, fluid mechanics and predicting the trajectories of light around black holes. They have worked extensively with undergraduate students on those problems over the past six years and found that the solution to the SIR epidemic model had a very similar mathematical structure. Although the authors haven't previously worked in the field of epidemiology, their previous work translated seamlessly to this new field.

"Many times, that's what we as applied mathematicians do—work at the boundaries of fields where people are not typically talking," said Weinstein. "We serve an important function to provide algorithms to support scientific inquiry and prediction. The technique we have developed here is general to many different fields."

The authors are now working on showing how their method can be applied to more complex models such as the SEIR epidemic model, which is similar to the SIR model but also predicts the population exposed to an epidemic.

More information: Nathaniel S. Barlow et al. Accurate closed-form solution of the SIR epidemic model, Physica D: Nonlinear Phenomena (2020). DOI: 10.1016/j.physd.2020.132540
Provided by Rochester Institute of Technology