Что такое ECDSA в биткоине?

Что такое ECDSA?

ECDSA (аббревиатура от Elliptic Curves Digital Signature Algorithm, алгоритм построения цифровой подписи с использованием эллиптических кривых) – это схема криптографии на основе эллиптических кривых (Elliptic Curve Cryptography или ECC).

Алгоритм ECDSA использует эллиптическую кривую и конечное поле для создания подписи данных таким образом, что третьи стороны могут верифицировать аутентичность подписи, а подписавшая сторона сохраняет эксклюзивную возможность создавать подпись. В случае биткоина подписываемые данные – это транзакция передачи права собственности.

Кто и когда разработал концепцию ECC?

Концепцию криптографии на основе эллиптических кривых независимо друг от друга предложили математики Нил Коблиц и Виктор С. Миллер в 1985 году. Хотя их модель стала прорывом в криптографии, ECC не использовалась широко до начала 2000-х, когда ее внедрили интернет-провайдеры.

Как ECC применяется в криптовалютах?

Криптография, лежащая в основе схем цифровых подписей криптовалют, позволяет осуществлять верификацию транзакций между двумя сторонами в децентрализованной сети.

ECC обладает значительным преимуществом над шифрованием по методу RSA. Размер ключа, используемого для ECC, гораздо меньше размера ключа, необходимого для RSA. При этом ECC обеспечивает тот же уровень безопасности. Хотя шифрование по методу RSA в наши дни гораздо шире используется в интернете, ECC – это более эффективная форма RSA, что и служит причиной использования этой криптографии в криптовалютах.

Кто и когда разработал ECDSA?

Концепцию ECDSA представил в 1992 году канадский математик и криптограф Скотт Ванстоун.

Какую задачу выполняет ECDSA?

Технология в основе биткоина переосмысливает концепцию права собственности. В традиционном смысле владеть чем-либо – домом, денежной суммой и т. д. – значит либо хранить (физически/юридически) этот объект лично, либо передать на ответственное хранение доверенной структуре (например, банку).

В случае биткоина все обстоит иначе. Сами биткоины не хранятся ни центрально, ни локально, ни одна структура не выступает в роли их кастодиана.

Биткоины существуют в качестве записей в блокчейне, копии которого распределяются сетью связанных компьютеров. «Владеть» биткоином означает иметь возможность передавать контроль над ним другому пользователю, создавая запись передачи в блокчейне. Что дает такую возможность? Доступ к паре ключей ECDSA – открытому и закрытому.

ECDSA имеет отдельные процедуры для подписи и для верификации. Каждая процедура – это алгоритм, состоящий из нескольких арифметических операций. Алгоритм подписи использует закрытый ключ, алгоритм верификации – открытый ключ.

Что такое эллиптическая кривая?

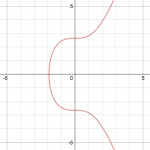
Эллиптические кривые имеют полезные свойства. Например, невертикальная линия, пересекающая кривую в двух точках, всегда будет пересекать третью точку на кривой. Другое свойство – невертикальная линия, касательная к кривой в одной точке, точно пересечет другую точку на кривой. Можно использовать эти свойства для определения двух операций: сложения точки и удвоения точки.

Для сложения точек, P + Q = R, через точки P и Q проводится прямая, которая пересекает кривую в третьей точке R.

Затем находится точка на кривой, симметричная третьей точке R относительно оси x. Точка R и будет считаться суммой P и Q. Пример:

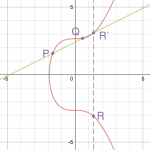
Аналогичным образом, при удвоении точки проводится прямая, касательная к эллиптической кривой в точке P, которая должна пересекать ее еще в одной точке R.

Точка R, симметричная R‘ относительно оси x, и будет считаться точкой удвоения P. Пример:

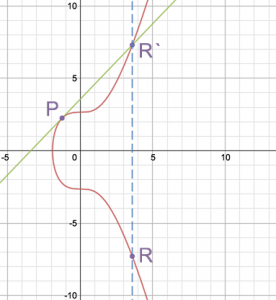
Вместе две эти операции используются для операции произведения на скаляр, R = a P, определяемой как добавление точки P к себе a раз. Например:

R = 7P
R = P + (P + (P + (P + (P + (P + P)))))

Процесс произведения на скаляр обычно упрощается посредством комбинации операций сложения и удвоения точек.

Например:

R = 7P
R = P + 6P
R = P + 2 (3P)
R = P + 2 (P + 2P)

Здесь 7P разделяется на два шага по удвоению точки и два шага по добавлению точки.

Что такое конечные поля?

Конечное поле в контексте ECDSA можно рассматривать как заданный диапазон положительных чисел, в который должен попадать каждый расчет. Любое число за пределами этого диапазона оборачивается таким образом, чтобы оно попадало в диапазон. Если результат операции выходит за пределы этого диапазона, то по окончании диапазона происходит возвращение к его началу, и расчет продолжается.

Самое простое – рассматривать этот процесс как расчет операции «остаток от целочисленного деления», или оператор modulus (mod). Например, 9/7 дает 1 с остатком в 2:9 mod 7 = 2. Здесь конечное поле – от 0 до 6, и все операции по модулю 7, над каким бы числом они не осуществлялись, дают результат, попадающий в этот диапазон.

Как происходит объединение кривых с конечными полями?

ECDSA использует эллиптические кривые в контексте конечного поля, которое значительно изменяет их внешний вид, но не фундаментальные формулы или особые свойства. То же самое уравнение, представленное на графике выше, в конечном поле по модулю 67 выглядит так:

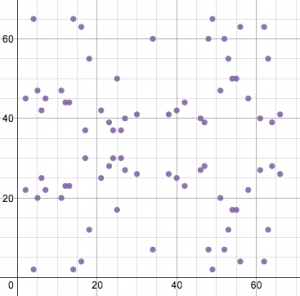
Теперь это набор точек, в котором все значения x и y являются целыми числами между 0 и 66. При этом кривая по-прежнему сохраняет свою горизонтальную симметрию.

Сложение и удвоение точек теперь визуально немного изменилось. Линии, вычерченные на этом графике, будут оборачиваться вокруг поля, сохраняя тот же наклон. Поэтому сложение точек (2, 22) и (6, 25) выглядит так:

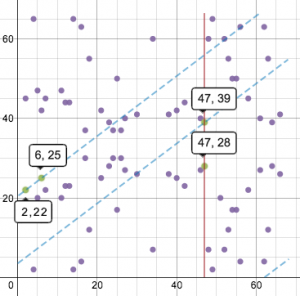
Оборачивающаяся прямая, проходящая через эти две точки, в итоге упирается в третью точку (47, 39), а симметричная ей относительно оси x будет (47, 28). Эта точка – результат операции.

Как ECDSA работает в биткоине?

Такой протокол, как биткоин, выбирает набор параметров для эллиптической кривой и репрезентацию его конечного поля, которая фиксирована для всех пользователей протокола.

Параметры включают само уравнение, простое значение модуля поля и базовую точку на кривой. Порядок базовой точки, которая не выбирается независимо, но является функцией других параметров, можно представить графически как число прибавлений точки к себе до тех пор, пока ее наклон не становится бесконечной (вертикальной) линией. Базовая точка выбирается так, что порядок – это большое простое число.

Для базовой точки простого модуля и порядка биткоин использует очень большие числа. Надежность алгоритма зависит от того, что эти величины огромны – это делает непрактичным использование брутфоса или инженерного анализа.

В случае биткоина:

Уравнение эллиптической кривой: y2 = x3 + 7

Простой модуль = 2256 – 232 – 29 – 28 – 27 – 26 – 24 – 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

Базовая точка = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Порядок = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

Данная реализация известна как secp256k1 и является частью семейства решений эллиптической кривой в области конечных полей, предложенных к использованию в криптографии.

Каковы недостатки ECDSA?

В ECDSA как текущем методе подписи в биткоине отсутствует нативная поддержка мультиподписей, поэтому их реализуют с помощью стандартизированного смарт-контракта Pay-to-Script-Hash (P2SH), предполагающего включение в блокчейн лишь хешей скриптов.

Это казалось бы случайное число определяет право собственности на монеты. В момент траты держатель раскрывает скрипт и ключ для расшифровки хеша одновременно. Затем каждый пользователь может использовать изначальный хеш для проверки истинности скрипта и исполнения условий траты. Однако при этом пользователи должны раскрывать все условия траты, включая и те, которые не были выполнены. Например, монеты могут быть потрачены тогда и только тогда, когда Боб и Алиса подпишут транзакцию, или Алиса подпишет ее самолично по истечению недели, или это сделает Боб, предоставив при этом секретное число.

Первая проблема такой модели – недостаток приватности. Для P2SH-транзакций необходимо, чтобы адреса начинались с цифры 3. Это дает блокчейн-аналитикам возможность распознать все P2SH-транзакции в сети и определить адреса, участвующие в мультиподписи.

Вторая проблема – большой массив данных для обработки, поскольку P2SH требует знания открытых ключей всех участников мультиподписи.

Эти проблемы решают схема подписей Шнорра и технология Taproot.