Investigating dynamics of democratic elections using physics theory

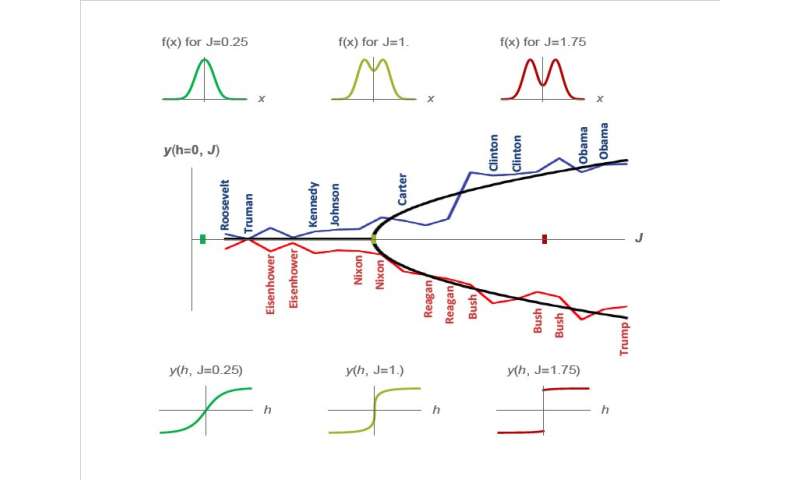
Sometimes, physics theories and constructs can also be used to study seemingly unrelated phenomena, such as social behaviors or dynamics. While human beings are not necessarily similar to specific physical particles, theories or techniques that physicists typically use to analyze behavioral patterns in atoms or electrons may aid the general understanding of large-scale social behaviors as long as these behaviors do not depend on small-scale details. Based on this idea, some researchers have started using physics theories to investigate social behaviors that take place during democratic elections.

Inspired by these previous efforts, two researchers at Massachusetts Institute of Technology (MIT) and the New England Complex Systems Institute have recently carried out a study to gain a better understanding of two specific dynamics of democratic elections that they discovered called negative representation and instability. Their paper, published in Nature Physics, suggests that some patterns observed during elections are comparable to the phase transition by which materials become ferromagnetic below their critical temperatures.

"Our study came about in the fall of 2016, because we were interested in how it was possible that the two potential election outcomes could be so drastically different," Alexander Siegenfeld, lead author of the paper, told Phys.org. "We started with models from economics, but realized that baked into the models were implicit assumptions that elections were stable, which didn't match what we observed in the real world."

The main objective of the study carried out by Siegenfeld and his advisor Yaneer Bam-Yam was to better understand some of the causes and consequences of electoral instability. When they first started conducting their research, however, they had no idea what they would find.

The first concept they investigated, known as negative representation, is a dynamic that occurs when a shift in electoral opinions results in a shift in electoral outcomes in the opposite direction to what was previously reported. The second notion they focused on is electoral instability, which is when an arbitrarily small change in electorate opinions can dramatically swing an election's final outcome.

"Negative representation means that the outcome is negatively sensitive to changes in that opinion: If the electorate shifts to the left, the outcome could shift to the right, or vice versa," Siegenfeld explained. "Instability means that a small change in positions of the electorate can cause large swings in the election outcome."

Siegenfeld and Bam-Yam realized that an election can be viewed as a process that takes the distribution of electorate political positions as inputs and gives the political position of the winning candidate as an output. The representation of specific political opinions of the electorate can then be defined by how sensitive the election outcome is to changes in these opinions.

More specifically, the researchers found that democratic elections can be modeled using a mathematical tool commonly used in physics studies, known as a functional, which is essentially a function of a function. Political representation can then be modeled using derivatives of the functional. In this context, they observed that electoral instability specifically occurs whenever the functional is discontinuous.

"I think the public discourse often takes electoral instability for granted or doesn't recognize its harm," Siegenfeld said. "In fact, a few decades ago in a 'be careful what you wish for' moment, political scientists lamented the similarity between Republicans and Democrats, even though that similarity is necessary for stability. I think this paper helps, firstly by mathematically identifying this phenomenon of elections being able to undergo a phase transition between stability and instability, and secondly, by showing that unstable elections always contain negative representation. This negative representation is one manifestation of why instability is so problematic."

Siegenfeld and Bar-Yam also found that a low voter turnout contributes to instability and negative representation, as the increasing polarization of the electorate can prompt a transition from a stable to an unstable regime, which resembles the phase transition through which some materials become ferromagnetic. This observation ultimately suggests that having a high voter turnout is important, not only because it allows more people's voices to be heard, but also because it contributes to a democracy's long-term stability.

Interestingly, when analyzing empirical data from past elections, the researchers found that presidential elections in the U.S. underwent a phase transition like the one described in their paper in the 1970s, which has caused them to become increasingly unstable. In other words, before the 1970s, center candidates would typically win presidential elections, but subsequently, this pattern radically changed. This change becomes apparent when observing the increasingly wider swings in the political positions of both Republican and Democratic candidates, which ultimately reflect a growing polarization of the electorate.

"Another key result of our study is that the primary system that we currently have in the U.S. can create instability (and therefore negative representation), even in the absence of other factors, suggesting the need for electoral reforms that bypass the two-party system, such as ranked-choice voting, which is currently used in Australia, Maine and a number of U.S. cities, including New York City, Cambridge and San Francisco."

The study carried out by Siegenfeld and Bar-Yam provides interesting new insight about the dynamics behind the formation of political opinions and of how these opinions can influence electoral results. Concurrently, it may also lay the foundation for new studies investigating similarities between large-scale electoral behaviors and physical systems.

"My plans for future research include applying methods and concepts from physics to better understand other political and economic problems, as well as to the general mathematical structures that characterize complex systems," Siegenfeld added. "I have recently posted an introduction to this field of applying physics to social systems on arXiv."

More information: Alexander F. Siegenfeld et al. Negative representation and instability in democratic elections, Nature Physics (2020). DOI: 10.1038/s41567-019-0739-6

An introduction to complex systems science and its applications. arXiv:1912.05088 [physics.soc-ph]. arxiv.org/abs/1912.05088

Journal information: Nature Physics

© 2020 Science X Network